Lissajous
Bei einigen Bildern in der Keetmann-Ausstellung fiel mir spontan der Begriff Lissajous-Figuren ein. Im Nachhinein ist mir eigentlich nicht klar, wieso mir der Name so spontan in den Sinn kam und warum ich diese Kurvenformen so plastisch vor Augen hatte.
Waren es Erinnerungen an den Physik-Unterricht in der Schulzeit ? Wohl nicht. In dem Physikbuch aus der Schulzeit : ”Höfling, Physik / Oberstufe” finde ich nichts darüber. Während des Studiums ? Auch nicht sehr wahrscheinlich. In der Physikbibel ”Gerthsen, Physik – Ein Lehrbuch zum Gebrauch neben Vorlesungen”, und das war exakt das Wissen, das Prof. Neuert uns damals zu vermitteln suchte, findet sich zwar das Stichwort ”Lissajoussche Figuren” aber im Text geht es nur kurz um Phasenverschiebung bei zwei harmonischen Schwingungen, die zueinander senkrecht stehen und als Abbildung gibt es nur Kreis und Ellipse. Bleibt als letzte Möglichkeit noch die Zeit als ich an der Wersi-Orgel gebastelt und viel mit dem Oszilloskop hantiert und gemessen habe.
Bei Wikipedia führt das Stichwort ”Lissajous” zu der Definition, zu den parametrischen Gleichungen und zu zahlreichen Bildern.
”Lissajous-Figuren sind Kurvengraphen, die durch die Überlagerung zweier harmonischer, rechtwinkelig zueinander stehender Schwingungen entstehen.”
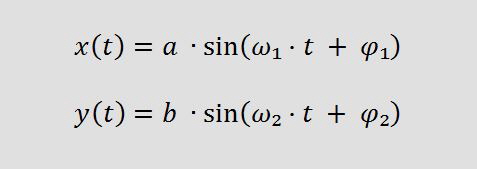
Es gibt auch ein Foto eines Oszilloskops mit einer Lissajous-Figur. Das war der Anlass solche Oszilloskop-Bilder für diesen Text selbst zu machen und damit herumzuspielen. Allerdings blieb mein Oszilloskop im Keller, bequemer geht es mit einer Emulation direkt auf dem Rechner.
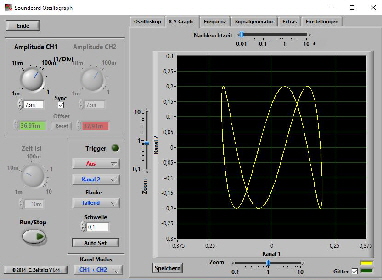
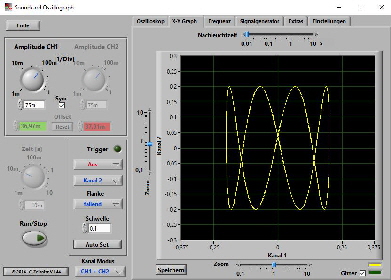
Die Figuren können durch die Parameter a,b,ω1,ω2,φ1 und φ2 in vielfältiger Weise variiert werden. a und b sind die Amplituden der beiden Schwingungen und skalieren die Figuren horizontal beziehungsweise vertikal. Die Komplexität der Kurven hängt wesentlich von den Frequenzen ω1,ω2 ab. Ist das Verhältnis ω1/ω2 rational (ganzzahliger Bruch) so erhält man geschlossene Figuren. Andernfalls sind die Kurven nicht periodisch. Variation der Phasenverschiebung φ1 und φ2 führt zu Drehungen der Kurven.
Fängt man erst einmal an damit zu spielen, entstehen viele, viele Kurven. Etliche davon sind in der externen Bildersammlung.
Eine andere nette Spielerei ergibt sich daraus, dass in dem Oszilloskop auch einen Funktionsgenerator integriert hat, der Dreieck- und Rechteckschwingungen liefert. Überlagert man diese mit Sinusschwingungen entstehen ganz andere spannende Kurvenformen.
Zwei Beispiele :
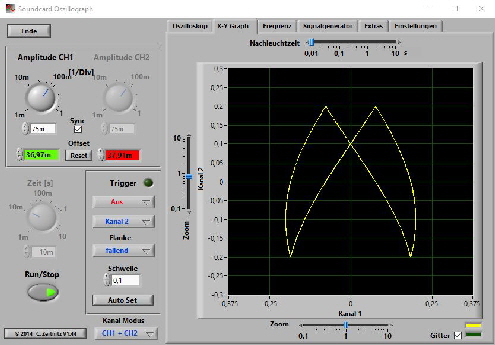
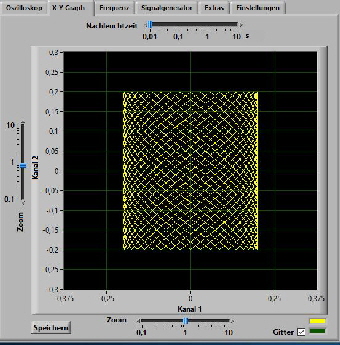
Wenn der Spieltrieb erst einmal geweckt ist ……
.......... mit anderen Grafikprogrammen lässt sich die Vielfalt auf die Spitze treiben.
Verschiedene Farben, dicke oder dünne Linien, Verknüpfung mit anderen Funktionen, dreidimensionale Darstellung und … und … und. Die Parameter Funktionen mit sin und cos waren ein herrliches Feld für Spielereien. Dann noch ein bißchen Photoshop in den ”Schüttelbecher” und es entsteht ein bunter Coctail. Beispiele dafür finden sich in der Bildershow.
Zum Schluss die Frage : gehört das alles in die Rubrik Mathematik und Natur(wissenschaft) oder ist auch etwas dabei was die momentane Zuordnung zu der Rubrik Mathematik und Kunst rechtfertigt ?
Noch ein Nachtrag : Für viele Themen, die auf diesen Seiten behandelt werden, gibt es ”GeoGebra- Dateien”, (*.ggb), mit denen an den Parametern der Gleichungen ”gespielt” werden kann.
GeoGebra ist eine Dynamische-Geometrie-Software, mit der geometrische Objekte gezeichnet und verändert werden können. Es können Gleichungen und zugehörige Parameter eingegeben und die Funktionen, Kurven und Objekte dynamisch dargestellt werden.
Funktioniert leider nur, wenn auf dem Rechner die Software (Freeware) installiert ist. Ich suche noch nach Auswegen, um das zu umgehen.
Trotzdem - Beispiele zum Ausprobieren :
Noch ein Nachtrag zum Nachtrag : ich habe dazugelernt. Man kann auch mit den Parametern in den Gleichungen experimentieren, ohne die Software auf dem Rechner installiert zu haben.
Hier ein Link zu einem zweidimensionalen System mit vielen Parametern, an denen man drehen kann : Lissajous_2exo
und auch ein einfaches 3-D-Modell : Liss_3D