Fibonacci in der Natur
Was haben diese Fotos gemeinsam ?









Nun, die Überschrift verrät es ja schon. Sie haben alle etwas mit den Fibonacci-Zahlen zu tun.
An den beiden folgenden Bildern erkennt man sehr gut das Muster aus links- und rechtsdrehenden Spiralen. Wenn man jetzt die nach rechts und nach links drehenden Spiralen zählt, erhält man 8 Spiralen nach rechts (rot) und 13 Spiralen nach links (blau). Dabei handelt es sich um zwei aufeinander folgende Fibonacci-Zahlen.

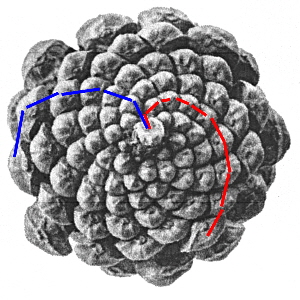
Diese spiralförmige Anordnung findet man bei den Samenständen vieler Pflanzen und ebenso auch bei der Anordnung von Blättern an einem Stängel oder Blütenblättern. Die Entstehung dieser Muster von rechts- und linksdrehenden Spiralen basiert auf dem goldenen Schnitt. Teilt man die 360° eines Kreises im Verhältnis des goldenen Schnittes, so ergibt sich ein Winkel von etwa 137,52°. Wird das Keimzentrum für den jeweils nächsten Samen oder das nächste Blatt an einem Stängel um diesen Winkel versetzt angeordnet so resultiert ein optimaler ”Bauplan” für die Pflanzen. Für die Samen kann so auf kleinstem Raum die größtmögliche Anzahl untergebracht werden. Für die Blätter bedeutet es, dass ein neu gebildetes Blatt nie genau über einem früher angelegten Blatt seinen Platz einnimmt. Dieses bedeutet eine optimale Nutzung des von oben einfallenden Lichtes, da sich die blätter am wenigsten gegenseitig beschatten aber auch keine Lücken entstehen, wo das Licht nicht genutzt wird.
Mathematisch beschreiben und auf dem Computer generieren lässt sich diese Anordnung von Punkten durch die Gleichungen
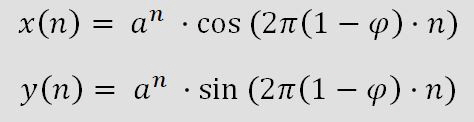
mit
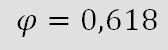
Durch diese Gleichungen ergeben sich Punkte, die auf einer einzigen logarithmischen Spirale mit dem Wachstumsfaktor a liegen. Auf dieser Trägerspirale sind die Punkte mit Winkelabständen von
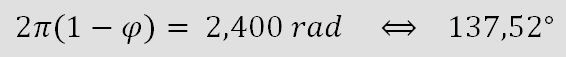
positioniert.
Bei der Darstellung links ist dieses in der vergrößerten Ansicht durch die eingezeichnete Spirale und die schwarz markierten ersten 5 Punkte zu erkennen. Es deutet sich aber schon an, was in dem Bild unten deutlich wird : die einzelnen Punkte werden nicht als auf einer Spirale liegend wahrgenommen, sondern das Gehirn sucht bei der Interpretation des Bildes nach Strukturen. Man erkennt links- und rechtsgekrümmte Spiralen auf denen die Punkte angeordnet sind. Zählt man die Spiralen so erhält man 21 nach rechts gekrümmte Spiralen und 13 Spiralen, die eine Linkskrümmung aufweisen.
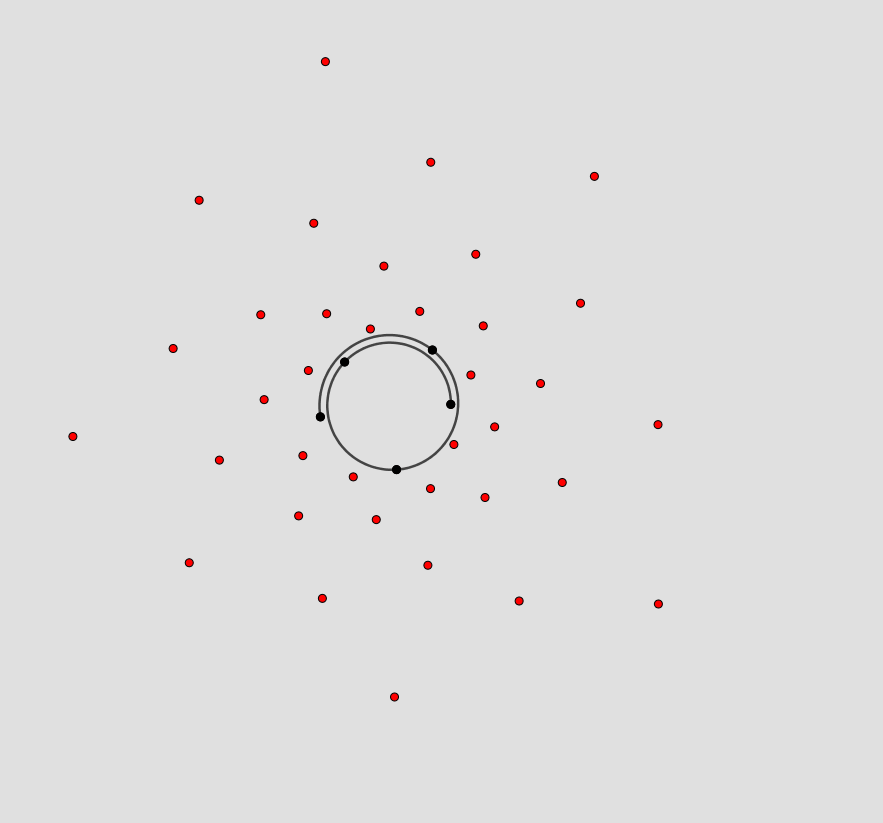

Auch dieses sind zwei aufeinanderfolgende Fibonacci-Zahlen.
Was passiert nun, wenn der volle Winkel nicht im Verhältnis des goldenen Schnittes geteilt wird, sondern in einem anderen irrationalen Verhältnis ?
Zum Beispiel im Verhältnis
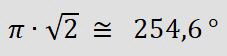
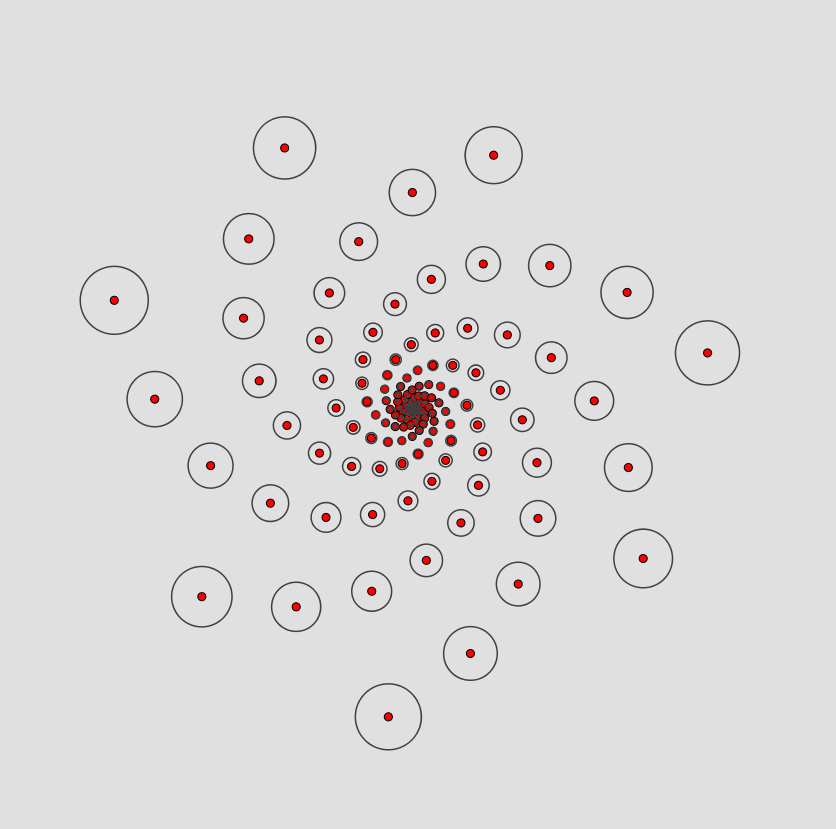
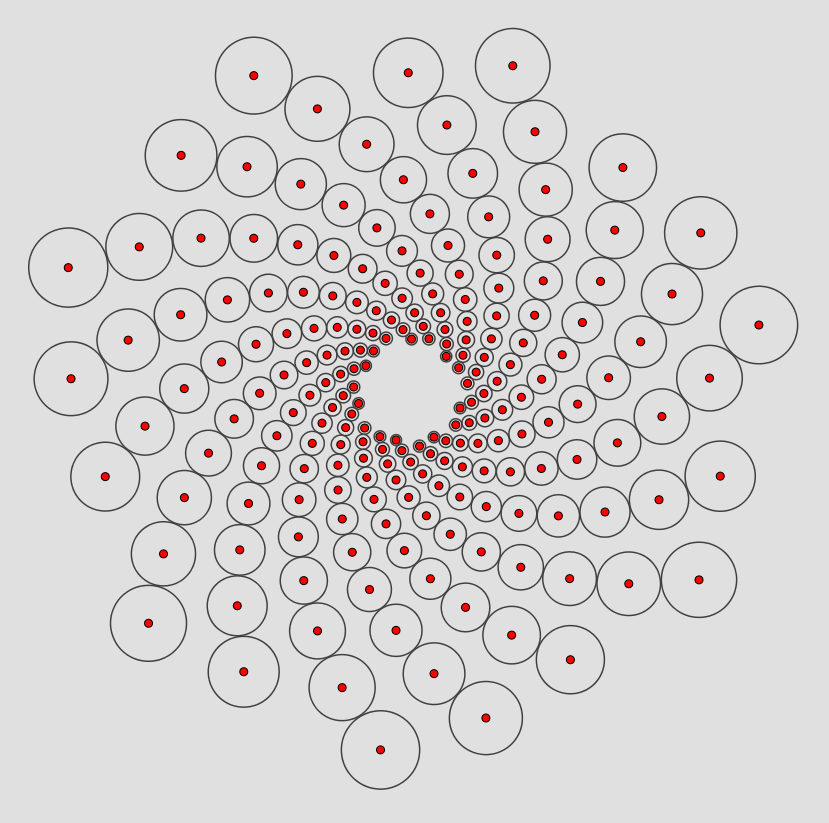
Die Anzahl der Spiralen ist vom Wachstumsfaktor a in obiger Gleichung abhängig. Mit einem Wachstumsfaktor von a = 1.03 sind im linken Bild 7 linksgekrümmte Spiralen leicht zu erkennen. Die rechtsgekrümmten Spiralen sind schwieriger auszumachen, aber mit etwas Geduld zählt man 10 Spiralen. Erstaunlicherweise ergibt 10 / 7 = 1,42 einen Näherungswert für ![]()
Im rechten Bild mit a= 1.01 ergeben sich 17 rechts- und 24 linksgekrümmte Spirale und mit 24 / 17 = 1,412 ein besserer Näherungswert für ![]()
Und bei einfachen Teilungsverhältnissen wie 360 / n mit n = 4,5,6,….?
Da kann man das Ergebnis fast erraten. 360 / 4 = 90° - es sind es 4 Strahlen jeweils im rechten Winkel zueinander. Bei 360 / 5 = 72° sind es dann 5 Strahlen
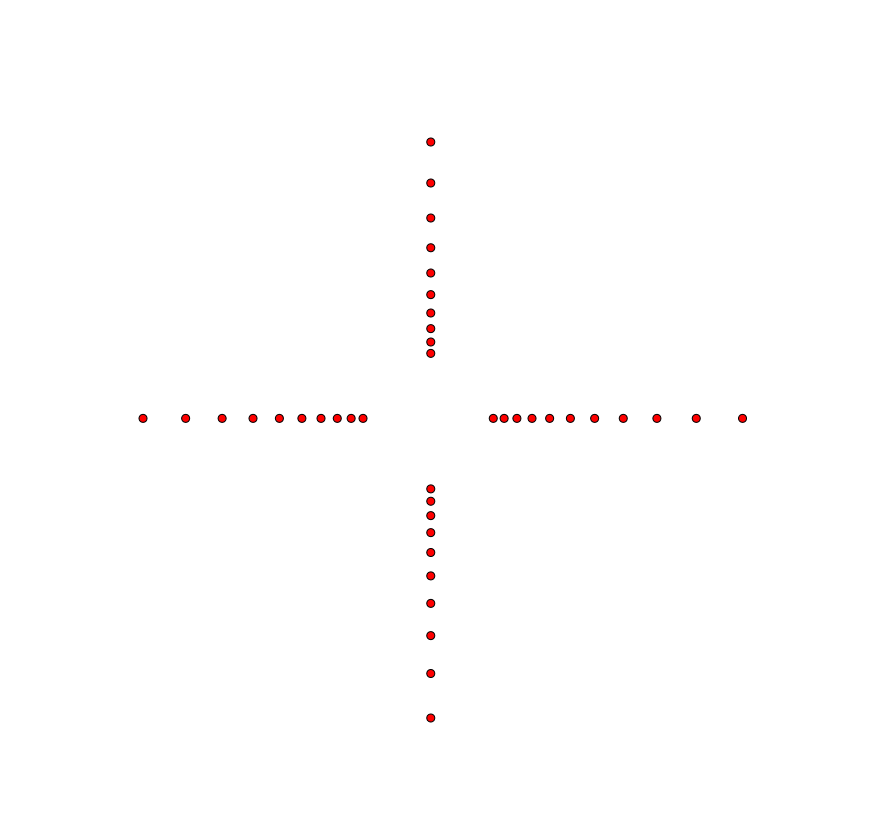
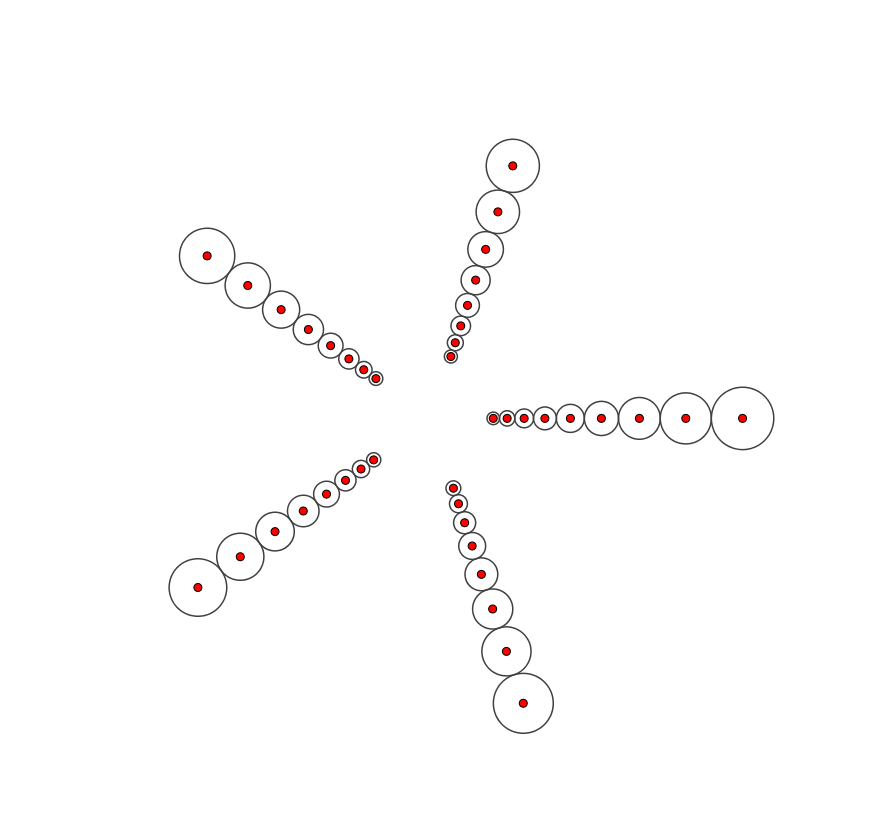
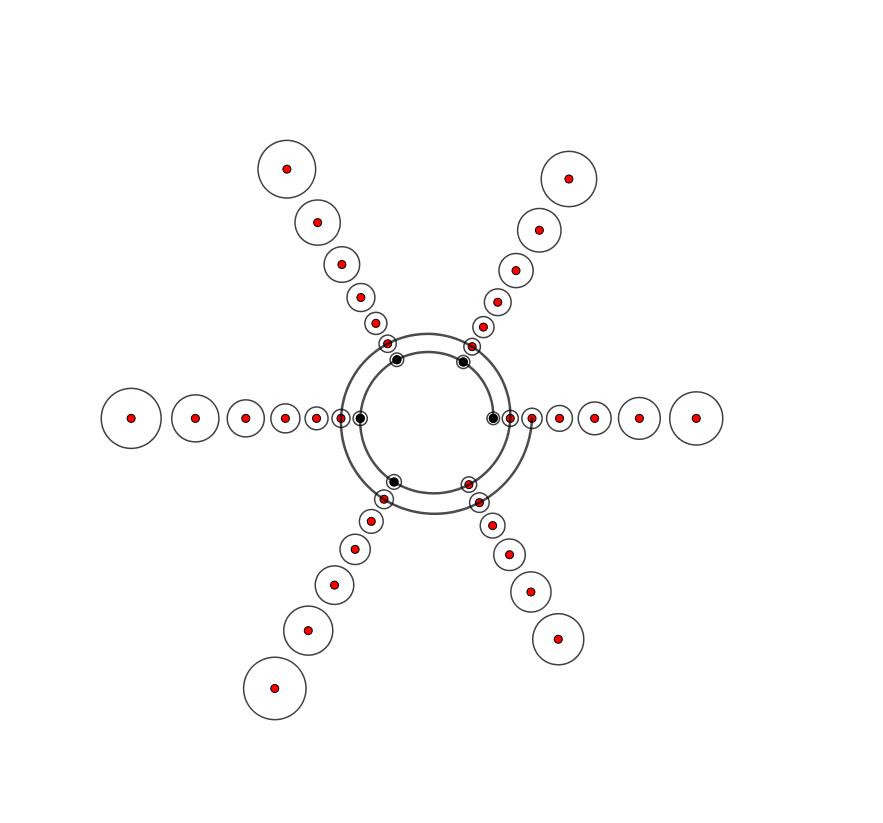
Bei 360 / 6 = 60° sieht man 6 Strahlen und hier ist die logarithmische Spirale auf der die Punkte liegen noch mit eingezeichnet
Jetzt ist der Spieltrieb erwacht !
Mit willkürlichen Werten für den Teilungswinkel, mit verschiedenen Wachstumsfaktoren a und dann mit zusätzlichen Mustern um die Punkte und verschiedenen Farben verziert, so entstehen oft ganz bizarre Muster. Ergebnisse, die bei dieser Spielerei herausgekommen sind habe ich in dem Bilderarchiv abgelegt. Ich lade zum Stöbern ein.