Fibonacci

Wenn man über den goldenen Schnitt irgendwo recherchiert oder auch jetzt hier bei mir liest, wie lange dauert es dann, bis man auf "Fibonacci" stößt ?

Genau, bis jetzt ! Bis zu dieser Überschrift.

Dabei hat Fibonacci (Fi(glio) die Bonacci = Sohn des Bonacci) im Jahr 1202 scheinbar nicht geahnt, in wie vielen Zusammenhängen die von ihm eingeführte Zahlenreihe steht.  F1

Jedenfalls hat er sie in seinem Buch "Liber Abaci" nur einmal, im Zusammenhang mit der "Kaninchenaufgabe", erwähnt.

Diese Aufgabe geht so:

Ein Kaninchenpaar wirft vom 2. Lebensmonat an in jedem Monat ein junges Kaninchenpaar. Es gilt für dieses Paar und alle Nachkommen die gleiche Regel. Also im ersten Monat noch kein Nachwuchs, aber danach Monat für Monat ein neues Pärchen. Wie viele Kaninchenpaare gibt es dann nach 12 Monaten ? (Randbedingung : die Kaninchen leben ewig und es verschwindet auch keins aus dem Gehege).

Anschaulich kann man das folgendermaßen darstellen :

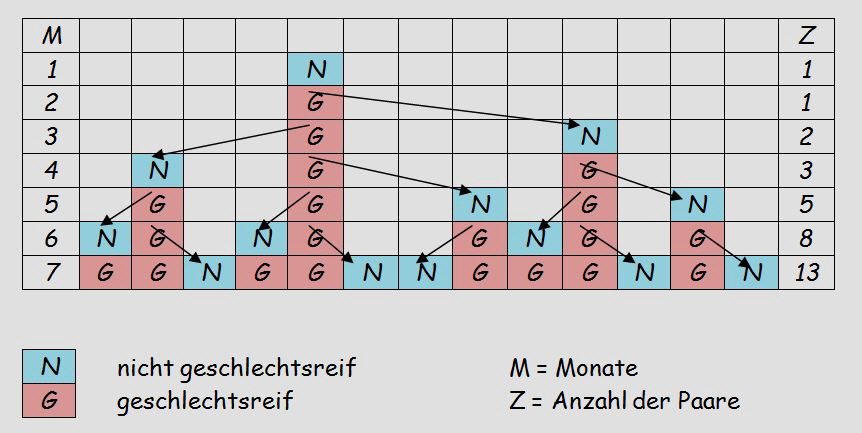
Das Bildungsgesetz der Fibonacci-Reihe lässt sich daran erkennen. Man addiert zwei aufeinander folgende Fibonacci-Zahlen und erhält die nächste :

1+1=2,  1+2=3,  2+3=5,  3+5=8,  5+8=13  und so fort.

Allgemein gilt also :  a_n + a_n+1  = a_n+2        mit den Startwerten a₁ = 1 und a₂ = 1.

Beziehungen der Fibonacci-Zahlen untereinander lassen oft überraschende Beziehungen erkennen.

Addiert man die Fibonacci-Zahlen beginnend bei a₁ bis a_n so ist die Summe gleich der übernächsten Fibonacci-Zahl minus 1.

                                   a₁ + a₂ + a₃ + ....... + a_n  =  a_n+2  -  1 

zum Beispiel

                                   1  +  1  +  2  +  3  +  5  =   12  =  13  -  1 

Vergleicht man bei drei aufeinanderfolgenden Fibonacci-Zahlen das Produkt aus der ersten und der dritten Zahl mit dem Quadrat der mittleren Zahl, so sind die Ergebnisse fast gleich. Sie unterscheiden sich lediglich um 1. Abwechselnd ist einmal das Produkt um 1 größer und einmal das Quadrat um 1 größer.

                                   a_n  ·  a_n  =  a_n-1  ·  a_n+1  +  (-1)^n-1   

Beispiele :

n = 2                            1  ·  1    =    1    ·   2    +  (-1)¹   =  2  -  1

n = 3                            2  ·  2   =    1   ·    3    +  (-1)²  =  3  +  1

n = 7                           13  ·  13 =    8  ·   21    +  (-1)⁶  = 168 + 1

Noch ein Beispiel aus vielen anderen Zahlenspielen ?

Addiert man die Quadrate der Fibonacci-Zahlen a₁ bis a_n, so ist die Summe dieser Quadrate gleich dem Produkt aus a_n mal a_n+1.

n=3 :  1 + 1 + 4 = 6       = 2 · 3 

n=4 :  1 + 1 + 4 + 9  = 15   = 3 · 5

n=5 :  1 + 1 + 4 + 9 + 25 = 40   = 5 · 8

n=6 :  1 + 1 + 4 + 9 + 25 + 64 = 104 = 8 · 13

Doch noch ein weiterer Zusammenhang. Diesmal zwischen Fibonacci und Pascalschem Dreieck also den Binomialkoeffizienten.

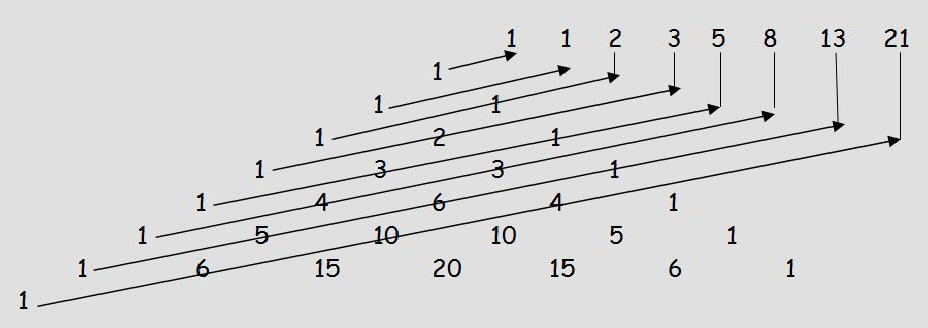
Die Summe der gezeichneten Diagonalen ergibt aufeinanderfolgende Fibonacci-Zahlen.

Die am häufigsten zitierte Beziehung ist jedoch das Verhältnis der Fibonacci-Zahlen mit dem goldenen Schnitt, also der Zahl   = 1,61803.......

Wenn man aufeinander folgende Fibonacci-Zahlen durcheinander dividiert, so ergeben sich mit steigendem a_n, wie die nachfolgende Tabelle zeigt, laufend genauere Näherungswerte für den Zahlenwert des goldenen Schnitts.

Der Grenzwert des Quotienten a_n+1/a_n geht gegen τ.

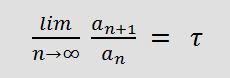
Dieser direkte Zusammenhang der Fibonacci-Reihe mit dem goldenen Schnitt führt dann noch in einen anderen Bereich, in dem dieses Zusammenspiel zu beobachten ist – in der Natur.

Dieses soll aber in einem separaten Kapitel betrachtet werden.